Binomisch formel

Tekst üüb Öömrang

A Binomisch Formeln san en wai uun a matematiik, am det moolnemen faan sumen ianfacher tu maagin. Jo halep uk bi't bröögreegnin mä sumen.

Det wurd binomisch komt faan bi (tau) an Nomen (nööm).

Formeln [Beårbe]

$(a + b)^n = \sum_{k=0}^{n} \binom n k a^{n-k} \cdot b^k$ , $n \in \mathbb{N}$

$(a+b)^2 = a^2 + 2 \cdot a \cdot b + b^2$	iarst Binomisch Formel (Plus-Formel)
$(a-b)^2 = a^2 - 2 \cdot a \cdot b + b^2$	ööder Binomisch Formel (Minus-Formel)
$(a+b) \cdot (a-b) = a^2 - b^2$	traad Binomisch Formel (Plus-Minus-Formel)

Troch moolnemen koon am a formeln bewise:

$(a+b)^2=(a+b)\cdot(a+b)=a \cdot a+a \cdot b+b \cdot a+b \cdot b=a^2+2 \cdot a \cdot b+b^2$

$(a-b)^2=(a-b) \cdot (a-b)=a \cdot a-a \cdot b-b \cdot a+b \cdot b=a^2-2 \cdot a \cdot b+b^2$

$(a+b) \cdot (a-b)=a \cdot a-a \cdot b+b \cdot a-b \cdot b=a^2-b^2$

A formeln halep uk bi't hoodreegnin:

Bispal 1

$37^2 = (30+7)^2 = 30^2 + 2 \cdot 30 \cdot 7 + 7^2 = 900 + 420 + 49 = 1369$

Bispal 2

$17 \cdot 13 = (15+2) \cdot (15-2) = 15^2 - 2^2 =225 - 4 = 221$

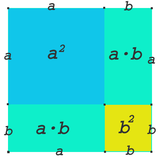
	Det Kwadroot as (a+b) lung an briad. Jo letj kwadrooten a² an b² paase diar jüst iin, an tau likedenang rochthuken a·b bliiw auer. Sodenang as $(a+b)^2=a^2+2\cdot a\cdot b+b^2$
	Uun't ööder bil as a² det blä kwadroot. Wan diarütj det kwadroot wurd skal, wat (a-b) lung an briad as, namst dü jo ruad rochthuken wech, diar a·b grat san. Nü heest dü diarmä oober b² tweisis wechnimen, diaram skal am det iansis weder diartutääl. Sodenang as $(a-b)^2=a^2-2\cdot a\cdot b+b^2$
	Uun't traad bil as a² det laacht- an jonkblä kwadroot. Woort det letj kwadroot b² wechnimen, an det rochthuk, wat auerblaft, oner bihinget, jaft det en rochthuk, wat (a-b) briad an (a+b) huuch as. Sodenang as $a^2-b^2=(a+b)\cdot (a-b)$